Wednesday, December 2, 2009
We have moved
I want you to be able to post to the blog, so I moved our blog to http://captncalc.edublogs.org/
Thursday, September 17, 2009
Quiz 3.1-3.4
I have just finished grading the indicated quiz. The average was an 80.8. This is very low. I know the material was difficult, but we need to clear this up after harvest because we will really start running when we get back. Derivatives is a large concept that has many pieces. If you miss one, you could be lost for awhile or never come back. I want all of you to stay in this class, so I want to work on getting your skills up to scratch when we get back. I think you should really pick up and study the first three sections a little over harvest. You are getting ready to head into the real world so you are in charge of assigning yourself some work to do so that you will be ready to continue on when we return.
Some ideas that bothered most of you.
- Limit definition of the derivative, how to use it and when.
- Graphing the derivative
- Product Rule
- Quotient Rule
- Derivative notation
- Basic algebra skills (I saw a lot of illegal cancellations)
Last year, I started mandatory tutoring sessions about this time. I hope that you will come in on your own accord. Mr. Sprague and other tutors are available in the Transitions center or after school, but they are not the same as me. They are usually very good, but sometimes I teach it differently then they do. In other classes, this is usually not a problem, but in this one it can be. I hope many of you will come visit me the first week back to pick up the missing concepts. If you don't visit me, and you should, I will probably come visit you.
Also, don't hesitate to place a comment on this blog or send me an email. I am pretty good at responding. I still have students from last year writing to me to help them solve some calculus problems. I am here to help. I will stay after school till about 5pm, if I am needed. Just let me know so we can solve this issue ahead of time and not try to catch up when it is too late.
Have a nice harvest vacation, but practice some calculus.
Some ideas that bothered most of you.
- Limit definition of the derivative, how to use it and when.
- Graphing the derivative
- Product Rule
- Quotient Rule
- Derivative notation
- Basic algebra skills (I saw a lot of illegal cancellations)
Last year, I started mandatory tutoring sessions about this time. I hope that you will come in on your own accord. Mr. Sprague and other tutors are available in the Transitions center or after school, but they are not the same as me. They are usually very good, but sometimes I teach it differently then they do. In other classes, this is usually not a problem, but in this one it can be. I hope many of you will come visit me the first week back to pick up the missing concepts. If you don't visit me, and you should, I will probably come visit you.
Also, don't hesitate to place a comment on this blog or send me an email. I am pretty good at responding. I still have students from last year writing to me to help them solve some calculus problems. I am here to help. I will stay after school till about 5pm, if I am needed. Just let me know so we can solve this issue ahead of time and not try to catch up when it is too late.
Have a nice harvest vacation, but practice some calculus.
Monday, September 14, 2009
Motion
Motion is a large topic of calculus and physics. In calculus, motion questions are used to evaluate a student's understanding of the difference quotient, derivatives, and integrals. For now we will focus on the first two, but we will look at integrals in time.
The whole show begins with a position function, s(t). If you want to find something's instantaneous velocity [v(t)], you just take the derivative of the position function. If you want to find something's instantaneous acceleration [a(t)], you just take the derivative of the velocity function. I equate these ideas to finding the tangent line, so I always remember to take the derivative.
We also talked about displacement. Displacement is your change in position. I always think about it as the distance from my starting point after I'm all done with the movement. "How far is it from where I began?"
We also talked about average values. Average velocity is the change in position divided by your change in time. Average acceleration is the change in velocity divided by your change in time. I just equate these ideas to the secant line, so I always remember what it is that I am doing.
I also asked that you look at example 6 on page 129. This talks about how derivatives are used in economics. In general, profit = revenue - cost or money in - money out. If you want to find the marginal revenue, the amount of money gained by producing one more unit or how the revenue is changing at that instant, you simply take the derivative or the revenue function. If you want to find the marginal cost, the extra cost of producing one more unit or how the cost is changing at that instant, you simply take the derivative or the cost function. If you want to find the marginal profit, you subtract the marginal cost from the marginal revenue.
The whole show begins with a position function, s(t). If you want to find something's instantaneous velocity [v(t)], you just take the derivative of the position function. If you want to find something's instantaneous acceleration [a(t)], you just take the derivative of the velocity function. I equate these ideas to finding the tangent line, so I always remember to take the derivative.
We also talked about displacement. Displacement is your change in position. I always think about it as the distance from my starting point after I'm all done with the movement. "How far is it from where I began?"
We also talked about average values. Average velocity is the change in position divided by your change in time. Average acceleration is the change in velocity divided by your change in time. I just equate these ideas to the secant line, so I always remember what it is that I am doing.
I also asked that you look at example 6 on page 129. This talks about how derivatives are used in economics. In general, profit = revenue - cost or money in - money out. If you want to find the marginal revenue, the amount of money gained by producing one more unit or how the revenue is changing at that instant, you simply take the derivative or the revenue function. If you want to find the marginal cost, the extra cost of producing one more unit or how the cost is changing at that instant, you simply take the derivative or the cost function. If you want to find the marginal profit, you subtract the marginal cost from the marginal revenue.
Thursday, September 10, 2009
Derivative Rules
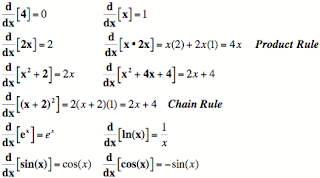
There are many rules that can be used to find the derivative of a function. These are quick rules that can be proved using the limit definition of the derivative, but once you know the rules you can use them to save time when finding the derivative. The six basic rules we looked at are shown below. These rules assume that c is a constant, u and v are functions in terms of x, and that the derivative exists for all x's in the domain of the function.
You must also be able to read the notation in the book. Below is a brief list of the notation that your book and many other mathematical texts use to identify the first-order derivative and its successors.
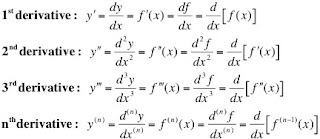
In the next sections, we will introduce more rules that will help us find the derivatives of trigonometric, logarithmic, and exponential functions.
You must also be able to read the notation in the book. Below is a brief list of the notation that your book and many other mathematical texts use to identify the first-order derivative and its successors.
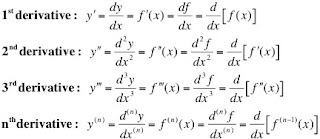
In the next sections, we will introduce more rules that will help us find the derivatives of trigonometric, logarithmic, and exponential functions.
Wednesday, September 9, 2009
GeoGebra
Today, we finished our study of the derivative using GeoGebra. We found the derivative of many functions using a graphical method. The graphical method involved creating a point B that had the coordinates (x,m), where x is the x-coordinate of the point on the function that the tangent line goes through and m is the slope of the tangent line. Point B traced out our derivative and then we were able to guess the derivative from the function.
We found the following derivatives:
The next step will be to develop rules so that we can find the derivative without using the limit definition of the derivative or having to rely solely on graphs.
We found the following derivatives:
The next step will be to develop rules so that we can find the derivative without using the limit definition of the derivative or having to rely solely on graphs.
Tuesday, September 8, 2009
GeoGebra
It is very unfortunate that our technology did not work so that we can get a visual of the derivative. The lesson was to connect the function with its derivative. We are going to start learning rules that will enable us to find the derivative much quicker than using the limit definition of the derivative. Remember, the derivative is a function that tells us the slope of our original function, everywhere. By the end of the week, we will have many skills in our repertoire that will allow us to find the derivative of many complex functions (more than just polynomials).
It is important that you keep GeoGebra at the top of the pile of useful tools (right next to the unit circle). The address for GeoGebra is http://www.geogebra.org/cms/ or you can click the word GeoGebra in the title of the post. At your home, you should be able to Webstart the program and create the worksheet like we tried to in class. This program can help you graph functions, trace the values, and copy the graphs into a document very easily. I suggest that you just play with the program a little.
Since our technology will not work individually, we will work on this tomorrow as a large group to see if we can figure out the derivatives from the tracing of the tangent lines to every point on the function. Hopefully, my computer will be able to complete this task, unlike yours.
It is important that you keep GeoGebra at the top of the pile of useful tools (right next to the unit circle). The address for GeoGebra is http://www.geogebra.org/cms/ or you can click the word GeoGebra in the title of the post. At your home, you should be able to Webstart the program and create the worksheet like we tried to in class. This program can help you graph functions, trace the values, and copy the graphs into a document very easily. I suggest that you just play with the program a little.
Since our technology will not work individually, we will work on this tomorrow as a large group to see if we can figure out the derivatives from the tracing of the tangent lines to every point on the function. Hopefully, my computer will be able to complete this task, unlike yours.
Friday, September 4, 2009
Differentiability
The derivative of a function exists if the left-hand derivative is equal to the right-hand derivative, just like with limits. There are only a few times that the derivative does not exist, and it is usually narrowed down to a specific point, or set of points.
The derivative fails to exist at a ...
1. Corner, like the one found in y=abs(x). This function is not differentiable at x=0. If you look at the left part of the function (x<0), y="x.">0), the function is described by the equation y= -x. The slope of the tangent line (the derivative) is -1. The two derivatives do not match, so the derivative does not exist at x = 0.
2. Cusp, like the one found in y = x^(2/3). If you look at this graphically you can see that the slope at x = 0 changes very quickly from positive to negative. We will look at the slope of this equation later when we have some more rules for derivatives.
3. Vertical tangent, like the one found in y = cuberoot(x). If you look at the graph of this function you will see that at x = 0, you will have a vertical tangent line. This is where I said you may want to use a small piece of paper to represent the tangent line. When you get around x = 0, your piece of paper will be pointing straight up, indicating a vertical tangent. Again, we will look at calculating this derivative (to the left and right of x =0) later on.
4. Discontinuity. We already studied discontinuities back in chapter 2. As a refresher, they are point (removable), infinite, oscillating, and jump. This means that if we find any discontinuities, our function will also not be differentiable for that particular x-value.
Now I gave you some instances, but it was merely a coincidence that our points where the functions were not differentiable were at x = 0, so don't fall into the trap of automatically thinking that is. Have a great long weekend.
The derivative fails to exist at a ...
1. Corner, like the one found in y=abs(x). This function is not differentiable at x=0. If you look at the left part of the function (x<0), y="x.">0), the function is described by the equation y= -x. The slope of the tangent line (the derivative) is -1. The two derivatives do not match, so the derivative does not exist at x = 0.
2. Cusp, like the one found in y = x^(2/3). If you look at this graphically you can see that the slope at x = 0 changes very quickly from positive to negative. We will look at the slope of this equation later when we have some more rules for derivatives.
3. Vertical tangent, like the one found in y = cuberoot(x). If you look at the graph of this function you will see that at x = 0, you will have a vertical tangent line. This is where I said you may want to use a small piece of paper to represent the tangent line. When you get around x = 0, your piece of paper will be pointing straight up, indicating a vertical tangent. Again, we will look at calculating this derivative (to the left and right of x =0) later on.
4. Discontinuity. We already studied discontinuities back in chapter 2. As a refresher, they are point (removable), infinite, oscillating, and jump. This means that if we find any discontinuities, our function will also not be differentiable for that particular x-value.
Now I gave you some instances, but it was merely a coincidence that our points where the functions were not differentiable were at x = 0, so don't fall into the trap of automatically thinking that is. Have a great long weekend.
Thursday, September 3, 2009
The Derivative
Today, we started our discussion on the derivative. The derivative is a function for the slope of the tangent line everywhere. We found the derivative using the limit definition that can be found on page 95. We found that if f(x) = x^2, then f'(x) = 2x. This means that the slope of the tangent line for f(x) = x^2 at x=3 is
f'(3) = 2(3) = 6.
We also spent some time looking at the graph of f'(x) as it related to f(x). For right now, we are only approximating the slopes of the given graph. Mostly, we look to see when the given graph has positive, negative, or zero slopes to help us determine the derivative graph. Soon, we will look at graphing the derivative of the function with a little more precision.
f'(3) = 2(3) = 6.
We also spent some time looking at the graph of f'(x) as it related to f(x). For right now, we are only approximating the slopes of the given graph. Mostly, we look to see when the given graph has positive, negative, or zero slopes to help us determine the derivative graph. Soon, we will look at graphing the derivative of the function with a little more precision.
Tuesday, September 1, 2009
Chapter 2 Review
Chapter 2 is finished. It is important that you understand the main concepts of this chapter as they will continue on throughout the course.
You should know...
1. How to find a secant line (average value), tangent line (instantaneous value) and normal line for any polynomial, trigonometric, or rational function.
2. A function is continuous at a point , a, iff the limit exists and approaches the same value as f(a).
3. Vertical asymptotes occur in rational functions when the denominator is zero.
4. Horizontal asymptotes occur at the value the infinite limits approach.
5. All the rules for limits (sum, difference, product, etc.)
6. The limit exists at a point iff the left hand limit matches the right hand limit.
7. How to find limits graphically using a tracing method with your pencil.
8. The Sandwich Theorem
9. How to find one-sided limits.
10. Types of discontinuities.
11. The Intermediate Value Theorem (IVT)
If you know all of the above skills, you are ready for your test. Good luck.
You should know...
1. How to find a secant line (average value), tangent line (instantaneous value) and normal line for any polynomial, trigonometric, or rational function.
2. A function is continuous at a point , a, iff the limit exists and approaches the same value as f(a).
3. Vertical asymptotes occur in rational functions when the denominator is zero.
4. Horizontal asymptotes occur at the value the infinite limits approach.
5. All the rules for limits (sum, difference, product, etc.)
6. The limit exists at a point iff the left hand limit matches the right hand limit.
7. How to find limits graphically using a tracing method with your pencil.
8. The Sandwich Theorem
9. How to find one-sided limits.
10. Types of discontinuities.
11. The Intermediate Value Theorem (IVT)
If you know all of the above skills, you are ready for your test. Good luck.
Monday, August 31, 2009
Secant/Tangent/Normal Lines
It is important for you to discern the difference between the aforementioned lines.
A secant line is a line that is drawn through two distinct points on a curve. To find the slope of the secant line you just find the change in y and divide by the change in x. Then all we need to do is plug it into point-slope form. y - yk =m (x - xk)
A tangent line is a line that is drawn through only one point on a curve. Right now, we find the slope of the tangent line by finding the limit as h goes to zero of the difference quotient (the change in y divided by the change in x) between our point x=a and a point immediately to the right, x=a+h. Once we do some algebra manipulation we will get a single number as the slope(m). Then all we need to do is plug it into point-slope form. y - yk =m (x - xk) This will be the equation for the tangent line through that single point (a, f(a))
A normal line is a line that is drawn through the same point on the curve as the tangent line was. It is perpendicular to the tangent, therefore its slope is -1/m. This means that only the slope needs to change from your tangent line equation when it is written in point-slope form.
y - yk =(-1/m)* (x - xk) This will be the equation for the normal line through that single point (a, f(a))
Example
A secant line is a line that is drawn through two distinct points on a curve. To find the slope of the secant line you just find the change in y and divide by the change in x. Then all we need to do is plug it into point-slope form. y - yk =m (x - xk)
A tangent line is a line that is drawn through only one point on a curve. Right now, we find the slope of the tangent line by finding the limit as h goes to zero of the difference quotient (the change in y divided by the change in x) between our point x=a and a point immediately to the right, x=a+h. Once we do some algebra manipulation we will get a single number as the slope(m). Then all we need to do is plug it into point-slope form. y - yk =m (x - xk) This will be the equation for the tangent line through that single point (a, f(a))
A normal line is a line that is drawn through the same point on the curve as the tangent line was. It is perpendicular to the tangent, therefore its slope is -1/m. This means that only the slope needs to change from your tangent line equation when it is written in point-slope form.
y - yk =(-1/m)* (x - xk) This will be the equation for the normal line through that single point (a, f(a))
Example
Sunday, August 30, 2009
Problem 13b from Friday
Above is the solution to problem 13b on page 88. I realized my mistake soon after class. I was in too much of a hurry to think what the question was actually posing. There are two and only two solutions for the standard absolute value equation (abs(x)). If x is positive, abs(x) has the equation y = x. The slope of the tangent line for any positive x on abs(x) is 1. If x is negative, abs(x) has the equation y = -x. The slope of the tangent line for any negative x on abs(x) is -1. This is shown above when x = -3. The relationship mentioned previously is the reason for the negative sign outside the parentheses in the second step. The rest of the steps are sequential and should be easy to follow. I apologize for the mistake and I will apologize in advance for any future ones. Obviously, I am human and that is a general flaw for all of humanity. I will try to minimize it as much as I can as far as calculus goes.
New to Blogging
I thought this would be a great way to communicate the day's lessons to you guys. You would be able to log in daily and check what it is that I taught, pick up any missing pieces, and catch up quickly if you miss class. It may also be a good way for you guys to post some questions about a concept. I am just hoping that I won't get too much spam and random comments, but I will never know unless I try. Posts will be updated period 3 (as long as the school does not block this website) and I will monitor the responses from home.
Subscribe to:
Posts (Atom)